Study Course Record/Codeit

Codeit - 자료 구조 (2) 기본 자료 구조들

hunteresting 2020. 7. 22. 11:35

# 하기 내용은 개인 기록을 위하여 정리한 강의 자료입니다.

 

  • 컴퓨터가 데이터를 저장하는 법

    1. 스토리지 vs 메모리

      • 자료구조의 목적 : 자료를 어떻게 구조화할지 고민해서 데이터를 효율적으로 사용

        • 자료 구조를 배우기 위해선 컴퓨터에 데이터가 어떻게 저장되는지에 대한 최소한의 지식은 있어야 함

      • 컴퓨터의 저장소

        • 스토리지

          • 데이터가 영구적으로 저장되는 곳

          • 사용자가 직접적으로 삭제하거나 컴퓨터에 큰 충격이 가해지지 않는 한 사라지지 않음

          • 데이터를 많이 저장할 수 있는 대신, 데이터를 저장하고 받아오는데 오래 걸림

          • 정확히 언제 사용할지 모르는 파일들을 저장

        • 메모리

          • 데이터를 임시로 저장하는 곳

          • 용량이 작은 대신 데이터를 저장하고 받아오는 것이 빠름

          • 지금 대충 사용해야하는 데이터를 저장

          • 자료구조는 데이터를 메모리에서 잘 사용하는 것이 목적

    2. RAM: Random Access Memory

      • 메모리의 특징

        • 일정한 칸으로 나눠져 있음

        • 각 칸에 데이터를 저장할 수 있음

        • 각 간은 자신만의 주소가 있음

      • RAM (임의 접근 메모리)

        • 임의 접근 : 저장 위치를 알면 접근할 때 항상 일정한 시간이 걸림

          • 메모리에 저장한 데이터 접근 시간 복잡도 : O(1) 

          • 순차 접근 : 저장된 위치까지 가는데 한 단계씩 거쳐야 함

          • 임의 접근이 순차접근보다 훨씬 효율적

    3. 메모리의 기본 단위: 바이트

      • 바이트(byte) : 메모리 한칸이 저장할 수 있는 가장 기본적인 용량의 단위

        • 바이트는 컴퓨터 저장 공간 용량을 나타내는 단위

        • 메모리 한 칸에 담기는 데이터 용량은 1바이트

    4. 레퍼런스

      • x=95

        • x는 95가 저장된 메모리 주소

        • "x는 95다"가 아닌 "x는 95를 가리킨다"가 맞는 표현

      • 레퍼런스 vs 주소?

        • 주소는 메모리의 실질적인 주소를 의미

        • 레퍼런스(reference)는 데이터에 접근할 수 있게 해주는 값으로 주소보다 조금 더 포괄적인 표현

        • 자료 구조를 배울 때는 "주소=레퍼런스"라고 생각해도 됨

      • 실제로 변수를 사용할 때는 파이썬이 저장된 값을 알아서 받아옴 

    5. 데이터의 주소

      • id 함수를 이용하여 저장한 데이터의 메모리 주소를 정수로 표현한 값을 알아낼 수 있음

         

         

      • 똑같은 주소에 저장돼 있는 데이터는 똑같은 데이터

        • 여러 변수가 같은 메모리를 가리키는 것을 Aliasing이라고 함

    6. 컴퓨터가 데이터를 저장하는 법 퀴즈

      • -

  • 배열

    1. 배열이란

      • C배열 vs 파이썬 list

        • C배열은 처음부터 크기가 고정되어 있으며, 같은 타입의 데이터만 담을 수 있음

          • 연속적인 메모리 주소를 사용

        • 파이썬 리스트는 계속해서 추가할 수 있고, 다양한 타입의 값을 담을 수 있음

          • 연속적인 메모리 공간에 저장되어있을 수도 있고, 아닐 수도 있음

          • 레퍼런스 4개를 저장 

    2. 배열 인덱스를 이용한 데이터 저장/접근법

      • 인덱스 i의 메모리 주소 = 시작주소 + 데이터 크기 * 인덱스

      • 배열 접근 연산 : O(1)

        • 어떤 내용이건 O(1)밖에 걸리지 않는 다는 것은 배열의 큰 장점

    3. 배열 탐색

      • 탐색 vs 접근

        • 접근은 인덱스를 통해 값을 찾음

        • 탐색은 특정 조건을 만족하는 값을 찾음

        • 배열에서 탐색은 접근보다 비효율적일 수 밖에 없음 (선형 탐색)

      • 배열 탐색 연산 : O(n)

    4. 정적 배열

      • 정적 배열은 처음 정의할 때 크기를 정해놓고, 정해진 크기 이상 값을 추가할 수 없음. (요소 수 제한)

      • 배열을 정의하면 메모리에서 쓸 수 있는 공간을 찾아야 하는데, 저장하려고 하는 데이터의 타입과 갯수에 따라 얼만큼의 공간이 필요한지 정해짐

        • 이 공간은 쭉 연결된 공간이어야만 함

    5. 동적 배열

      • 동적 배열(Dynamic Array)은 꽉 차도 계속 추가할 수 있음. (요소 계속 추가 가능)

        • 정적 배열로 만들어진 자료 구조

        • 정적 배열의 크기를 상황에 맞게 조절

        • 배열이 꽉 찼는데 더 추가해야하는 경우, 더 큰 크기의 새로운 배열을 만들고 기존 배열을 복사해오는 방식

    6. 파이썬 리스트(동적 배열)의 비밀

      • 동적 배열을 자료형으로 제공하는 대부분의 언어들은 실제 하용하는 배열의 크기와 상관없이 저장해 놓은 공간만 사용할 수 있게 처리를 해줌

    7. 동적 배열 추가 연산 시간 복잡도

      • 추가 연산(append operation) : 배열의 가장 끝에 새 값을 추가하는 것

        • 정적 배열에 남는 공간이 있는 경우 O(1)의 시간복잡도를 가짐. (인덱스를 이용하여 접근)

        • 정적 배열이 꽉 찼을 때는 O(n)의 시간 복잡도를 가짐

    8. 분할 상환 분석 개념

      • 분할 상환 분석 (Amortized Analysis) 

        • 같은 동작을 n번 했을 때 드는 시간이 x일 때 동작을 한번 하는 데 걸린 시간은  x/n

        • 시간 복잡도를 최악의 경우로 이야기 하지 않고 평균을 내서 이야기하기 때문에 보다 합리적인 시간복잡도를 구할 수 있음

    9. 분할 상환 분석 적용

      • 추가 연산을 연속으로 n번 하고, 가장 마지막에 옮겨 저장한 데이터 요소 수를 m이라고 할 때

        • 복사해서 저장하는 데 걸리는 총 시간이 2m-1이고

        • m은 n보다 작음

        • 정리해서 말하면, 연속으로 추가 연산을 n번 하면 데이터를 옮겨서 저장하는데 걸리는 총 시간은 2n보다 작음

      • 동적 배열의 추가 연산의 시간분석도는 최악의 경우로 가정하여 O(n)이지만, 분할 상환 분석으로 생각할 경우 O(n)/n, 즉 O(1)이 됨

      • 최악의 경우보다 분할 상환 분석을 한 시간 복잡도가 더 적다면, 분할 상환 분석을 한 시간 복잡도를 사용

    10. 동적 배열 삽입 연산

      • 삽인 연산 (insert operation) : 배열의 아무 위치에나 새로운 데이터를 더하는 것

        • 정적 배열에 남는 공간이 있는 경우 O(n)의 시간 복잡도를 가짐

        • 정적 배열이 꽉 찼을 때는 O(n)의 시간 복잡도를 가짐

    11. 동적 배열 삭제 연산

      • 삭제 연산 : 동적 배열의 특정 위치에 있는 데이터를 지움

        • 최악의 경우 O(n), 최선의 경우 O(1)이 걸림

    12. 동적 배열 크기 줄이기

      • 삭제 분할 상환 분석을 적용하면 맨 끝 데이터 삭제 연산도 O(1)이 걸린다고 할 수 있음

    13. 배열과 동적 배열 정리/비교

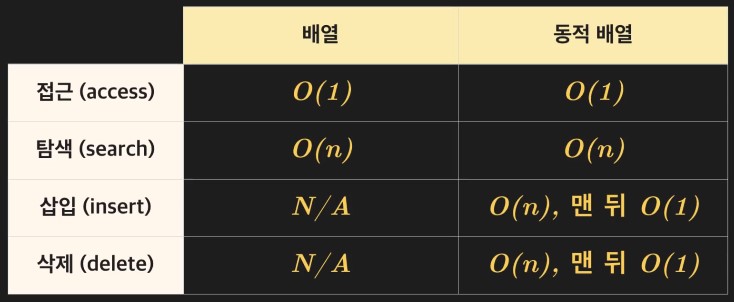
      • 연산 & 시간 복잡도

        • 접근과 탐색 연산은 배열과 동적 배열 모두 사용 가능

        • 배열에서는 삽입과 삭제를 사용할 수 없음

      • 낭비하는 공간

        • 배열은 크기가 고정되어 있기 때문에 낭비하는 공간이 없음

        • 동적 배열은 공간을 낭비할 수도 있고 안 할 수도 있음

          • 새로운 배열을 만들어야할 때마다 n-2만큼의 공간이 낭비됨 (O(n))

    14. 정적 배열에 삽입과 삭제를 못하는 이유

      • -

    15. 배열 퀴즈

      • -

  • 링크드 리스트

    1. 링크드 리스트 개념

      • 연결 리스트(Linked List)

        • 데이터를 순서대로 저장

        • 요소를 계속 추가할 수 있음

        • 노드라는 단위의 데이터를 저장하고 데이터가 저장된 각 노드들을 순서대로 연결시켜서 만든 자료구조

    2. 링크드 리스트 프로그래밍적으로 생각하기

      • 노드(Node)

        • 각 노드는 하나의 객체로 표현됨

        • data와 next라는 속성을 가짐

          • data에는 저장하고 싶은 정보를 적음

          • next는 다음 노드에 대한 레퍼런스를 저장

        •          링크드 리스트의 시작점 역할을 하는 노드를 head 노드라고 함  (마지막 노드는 tail 노드)

          • 헤드 노드만 있으면 메모리 여기저기에 흩어져 있는 다른 노드들을 연결지어서 순서를 저장할 수 있음

    3. 노드 클래스 만들기

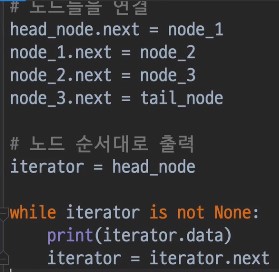
    4. 간단한 링크드 리스트 만들기

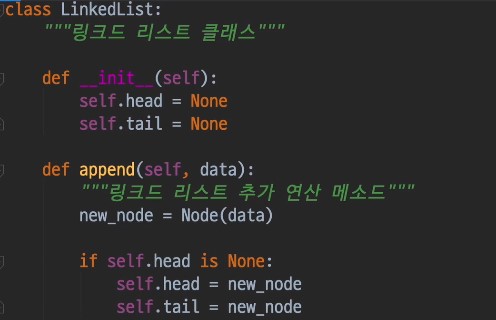
    5. 링크드 리스트 추가 연산

    6. 링크드 리스트 __str__메소드

      • 출력 결과 : | 2 | 3 | 5 | 7 | 11 |

    7. 링크드 리스트 접근

      • 배열 접근 연산 : 특정 위치에 저장한 데이터를 가지고 오거나 바꿔주는 연산

      • 링크드 리스트도 배열과 마찬가지로 접근 연산을 사용할 수 있으나, 링크드 리스트의 경우 특정 위치에 있는 노드를 리턴하는 연산이 됨

        • 링크드 리스트는 레퍼런스를 통해 순서를 저장하기 때문에 한번에 원하는 위치의 데이터에 접근할 수 없음

        • 인덱스 x에 있는 노드에 접근하려면 head에서 다음 노드로 x번 가면 됨

        • 인덱스를 이용해서 링크드 리스트에 접근할때는 배열에서 처럼 효율적이지 않음

          • 시간 복잡도 : O(n)

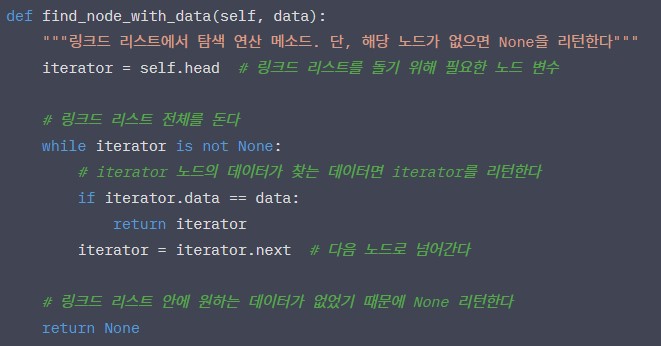
    8. 링크드 리스트 탐색 연산

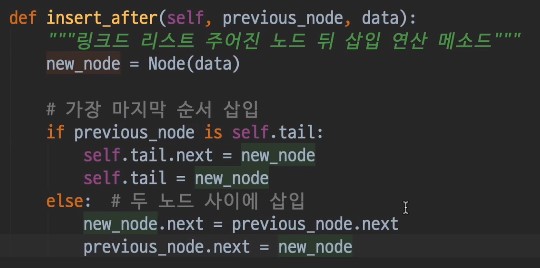
    9. 링크드 리스트 삽입 연산

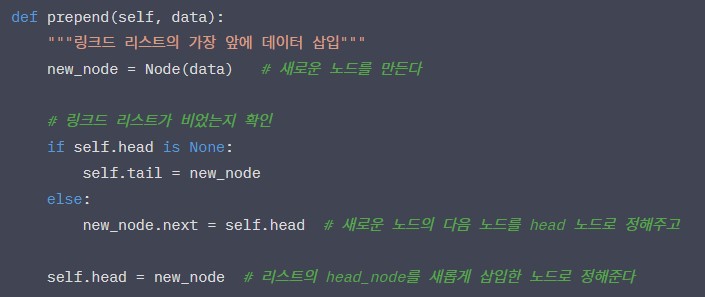
    10. prepend: 링크드 리스트 가장 앞 삽입

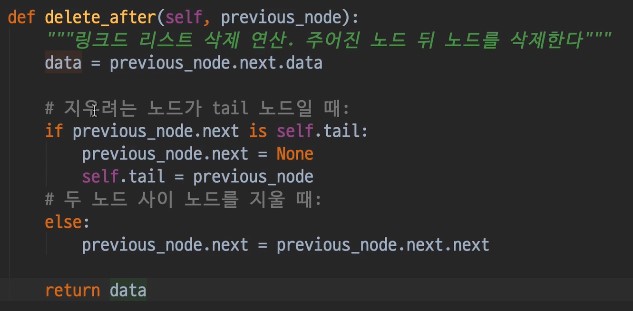
    11. 링크드 리스트 삭제

        • 링크드리스트에서 데이터를 삭제할 때는, 삭제한 데이터를 리턴해주는 것이 관습 

    12. popleft: 링크드 리스트 가장 앞 삭제

    13. 링크드 리스트 시간 복잡도

      • 접근 연산 : O(n)

        • 링크드 리스트 안에 있는 노드의 수가 n일때, 마지막 순서에 있는 노드에 접근해야하는 최악의 경우에는 head 노드에서 총 n-1번 다음 노드로 가야함

      • 탐색 연산 : O(n)

        • 링크드 리스트의 탐색연산은 선형 탐색을 사용하므로, 리스트 안에 찾으려는 데이터가 없거나 마지막에 있는 경우 n개의 노드를 전부 봐야 함

      • 삽입/삭제 연산 : O(n)

        • 삽입, 삭제할 인덱스의 주변 노드들에 연결된 레퍼런스만 수정하기 때문에 이 연산들을 실행하는데 걸리는 시간은 특정 값에 비례하지 않고 항상 일정함 (O(1))

        • 그러나 현실적인 삽입/삭제 시간 연산도의 경우, head와 tail노드를 제외하고는 접근 연산을 통해 나머지 노드를 가져와야하기 때문에 O(n+1)의 시간복잡도를 가짐

        • 링크드 리스트 가장 뒤 노드 삭제 연산은 나머지 세 연산만큼 효율적으로 할 수 없음

    14. 더블리 링크드 리스트

      • 싱글리 링크드 리스트 : 각 노드가 다음 노드에 대한 레퍼런스만 갖는 경우

      • 더블리 링크드 리스트 : 각 노드가 앞 노드와 뒤 노드에 대한 레퍼런스를 모두 가지고 있음

    15. 더블리 링크드 리스트 겹치는 메소드

      • __init__, 접근연산, 탐색연산, __str__ 메소드가 싱글리 링크드 리스트와 동일함

    16. 더블리 링크드 리스트 추가 연산

    17. 더블리 링크드 리스트 삽입 연산 개념

      • -

    18. 더블리 링크드 리스트 삽입 연산 구현

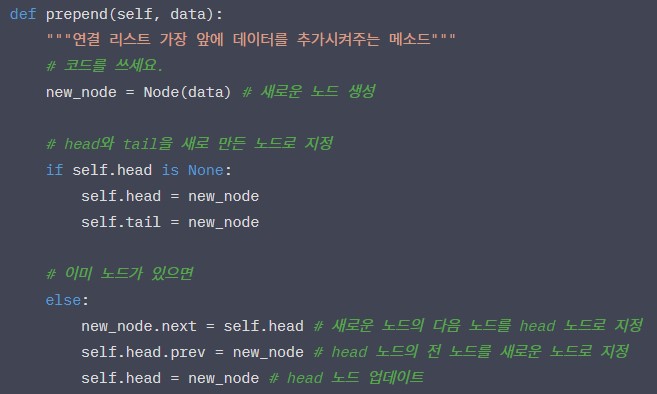
    19. 더블리 링크드 리스트 prepend 메소드

    20. 더블리 링크드 리스트 삭제 연산 개념

      • -

    21. 더블리 링크드 리스트 삭제 연산 구현

    22. 더블리 링크드 리스트 시간 복잡도

      • 접근/탐색 연산 : 싱글리 리스트와 동일하게 O(n)

      • 삽입/삭제 연산 : O(n)

        • 싱글리 리스트와 동일하게 접근 또는 탐색을 통해 특정 노드에 접근해야함

    23. 싱글리 vs 더블리 링크드 리스트

      • 둘 다 공간복잡도가 O(n)이지만, 실제로는 더블리 리스트가 싱글리 리스트의 두배이므로, 공간활용도를 최적화 하고싶다면 싱글리리스트를 사용하는 것이 좋음

    24. 링크드 리스트 퀴즈

      • 가장 앞 순서에 데이터를 많이 삽입해야 되는 경우에는 싱글리 리스트가 동적 배열보다 더 효율적임

  • 해시 테이블

    1. key - value 데이터

      • 하나의 key와 그 key에 해당하는 value를 합쳐서 : key-value 쌍

      • 하나의 key에는 하나의 value

    2. Direct Access Table

      • Direct Access Table : 인덱스를 키로 이용해서 데이터를 저장하고, 가지고 오는 방식

        • key(인덱스)를 이용한 value 접근 : O(1)

        • 효율적으로 key-value 쌍을 저장하고 가져올 수 있음

        • 낭비하는 공간이 많음

    3. 해시 테이블 개념

      • 해시 테이블 (Hash Table) : 해시 함수와 테이블을 같이 사용하는 개념

        • 해시 함수 : 특정 값을 원하는 범위의 자연수로 바꿔주는 함수

        • 키를 해시 함수에 넣고 배열의 인덱스에 집어넣는 방식

          1. 고정된 크기의 배열을 만듬

          2. 해시 함수를 이용하여 key를 원하는 범위의 자연수로 바꿈

          3. 해시 함수 결과 값 인덱스에 key-value 쌍을 저장

    4. 해시 함수

      • 해시 함수의 조건

        • 한 해시 테이블의 해시 함수는 결정론적이어야 함 (똑같은 key를 넣었을 때는 항상 똑같은 결과가 나와야 함)

        • 결과 해시 값이 치우치지 않고 고르게 나옴 (아무 숫자나 넣었는데 항상 똑같은 수만 나오면 안됨)

        • 빨리 계산할 수 있어야 함 (해시 테이블은 모든 연산을 할 때 마다 해시 함수를 써야하기 때문에 해시 함수가 비효율적이면 해시 테이블도 비효율적일 수 밖에 없음)

      • 해시 함수 만드는 방법

        • 나누기 방법 : 자연수 key를 해시 테이블의 크기로 나눈 나머지를 리턴. (가장 직관적이면서 쉬운 방식)

        • 곱셈 방법 : 0<a<1인 아무값 a를 정한 후, a에 key를 곱함. 이때 정수 부분은 버리고 소수 부분만 남겨서 남은 소수 부분에 배열의 크기를 곱함

    5. 파이썬 hash 함수

      • 파이썬에서도 hash함수를 제공

        • 우리가 배운 함수와 다르게, 파이썬 해시 함수는 파라미터로 받은 값을 그냥 아무 정수로만 바꿔주는 함수임

        • 서로 다른 두 값을 파라미터로 넣었을 때 같은 정수가 리턴될 수 없음

          • 데이터를 자신만의 고유한 정수 값으로 바꿔주는 함수

        • 불변(immutable) 타입 자료형에만 사용 가능

          • ex. 불린형, 정수형, 소수형, 튜플, 문자형

      • 해시 테이블을 직접 구현할 때 hash 함수를 사용하면 해시 테이블에 저장할 수 있는 종류의 데이터를 더 폭넓게 늘릴 수 있음

    6. 해시 테이블 충돌과 Chaining 개념

      • 충돌 (Collision) : 이미 사용하고 있는 인덱스에 새로운 key-value 쌍을 또 저장해야하는 경우

      • Chaining

        • 충돌이 일어나면, 그 값들을 최사슬처럼 엮는..

        • 배열 인덱스에 데이터를 연결시켜 주는 구조인 링크드 리스트를 저장해서 충돌 해결

    7. Chaining에서 사용하는 링크드 리스트

       

      •  

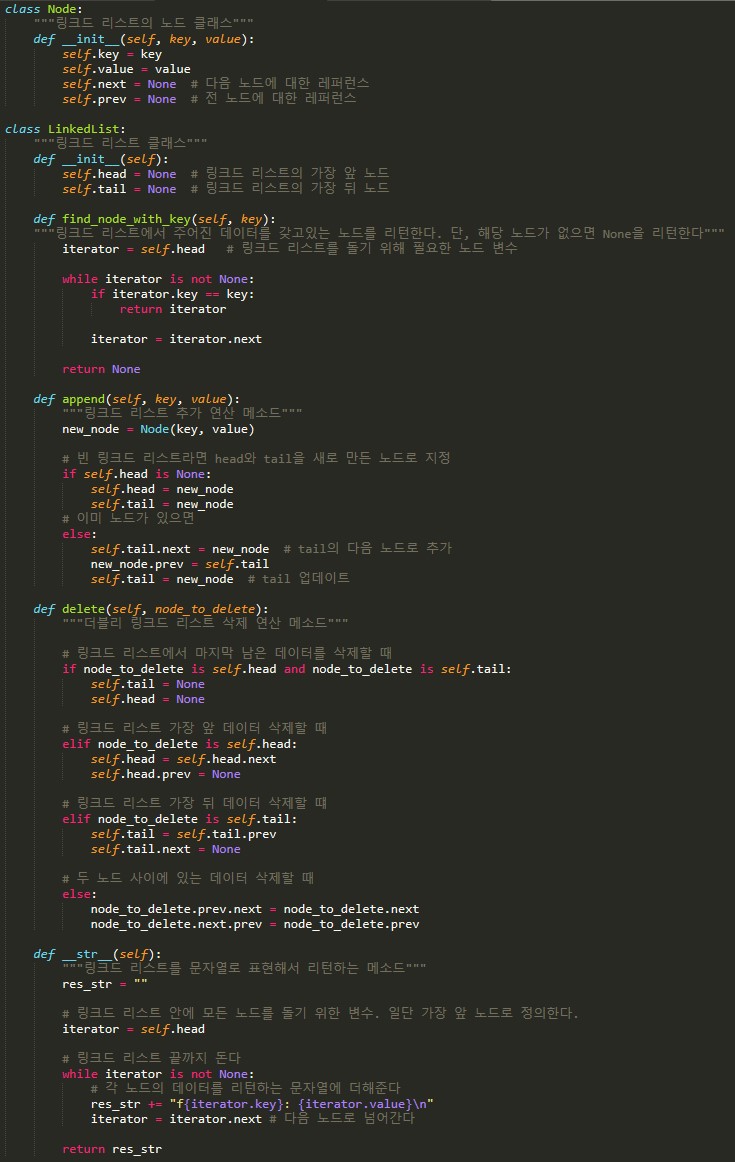
    8. Chaining을 쓰는 해시 테이블 탐색 연산

      • 해시 테이블은 데이터의 순서 관계를 저장하지 않기 때문에, 접근 연산이 없음

      • 해시 테이블의 탐색 연산 : 원하는 key에 해당하는 value를 찾는 연산

         

         

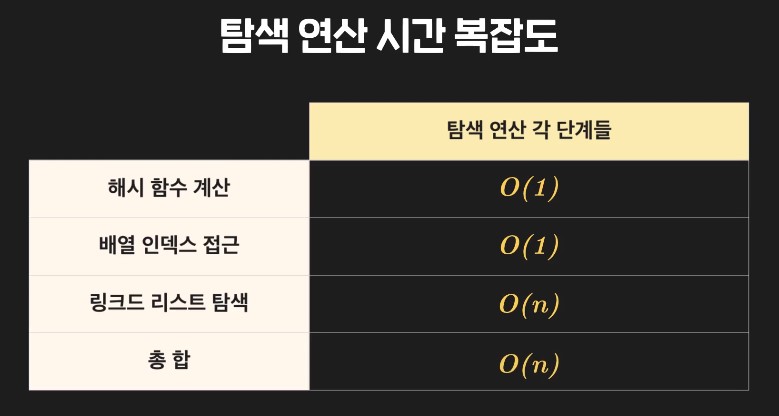
    9. Chaining을 쓰는 해시 테이블 삽입 연산

      • 해시 테이블의 삽입 연산 : key-value 데이터 쌍을 저장, 또는 수정

        • 기존에 있는 키가 탐색될 경우, 새로운 값으로 치환

        • 탐색에 실패할 경우(동일한 키가 없는 경우), 링크드 리스트의 가장 뒷쪽으로 배치

           

           

    10. Chaining을 쓰는 해시 테이블 삭제 연산

      • 해시 테이블의 삭제 연산 : 원하는 key에 대한 key-value 데이터 쌍을 삭제

         

         

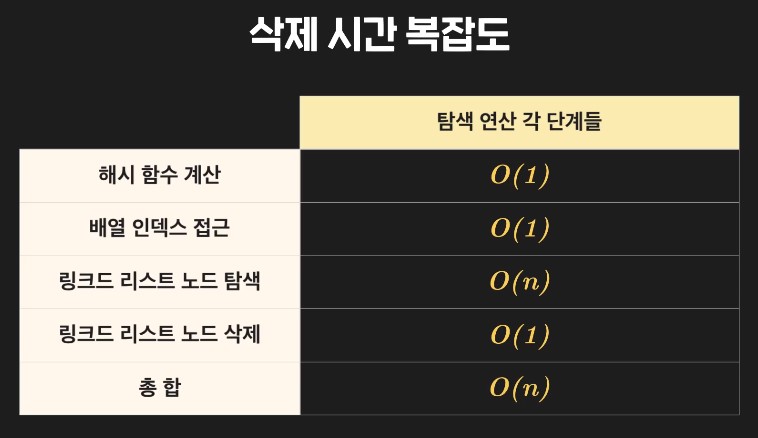
    11. (중요!)Chaining을 쓰는 해시 테이블 평균 시간 복잡도

      • 탐색/저장/삭제 연산의 평균 시간복잡도는 O(n)이지만, 모든 key-value쌍이 하나의 인덱스에 저장되는 최악의 경우가 발생할 확률은 매우 낮음

        • 평균적으로 걸리는 시간 = 해시 테이블에 총 들어가 있는 key-value쌍의 수 / 해시 테이블이 사용하는 배열의 크기

        • 해시 테이블을 만들때 항상 충분히 여유롭게 총 저장하는 key-value쌍 수와 해시 테이블이 사용하는 배열의 크기를 비슷하거나 작다고 가정할때, 해시 테이블의 시간 복잡도는 모두 O(1)이라고 할 수 있음

    12. Chaining을 쓰는 해시 테이블 구현 1

      • -

    13. Chaining을 쓰는 해시 테이블 구현 2

       

      •  

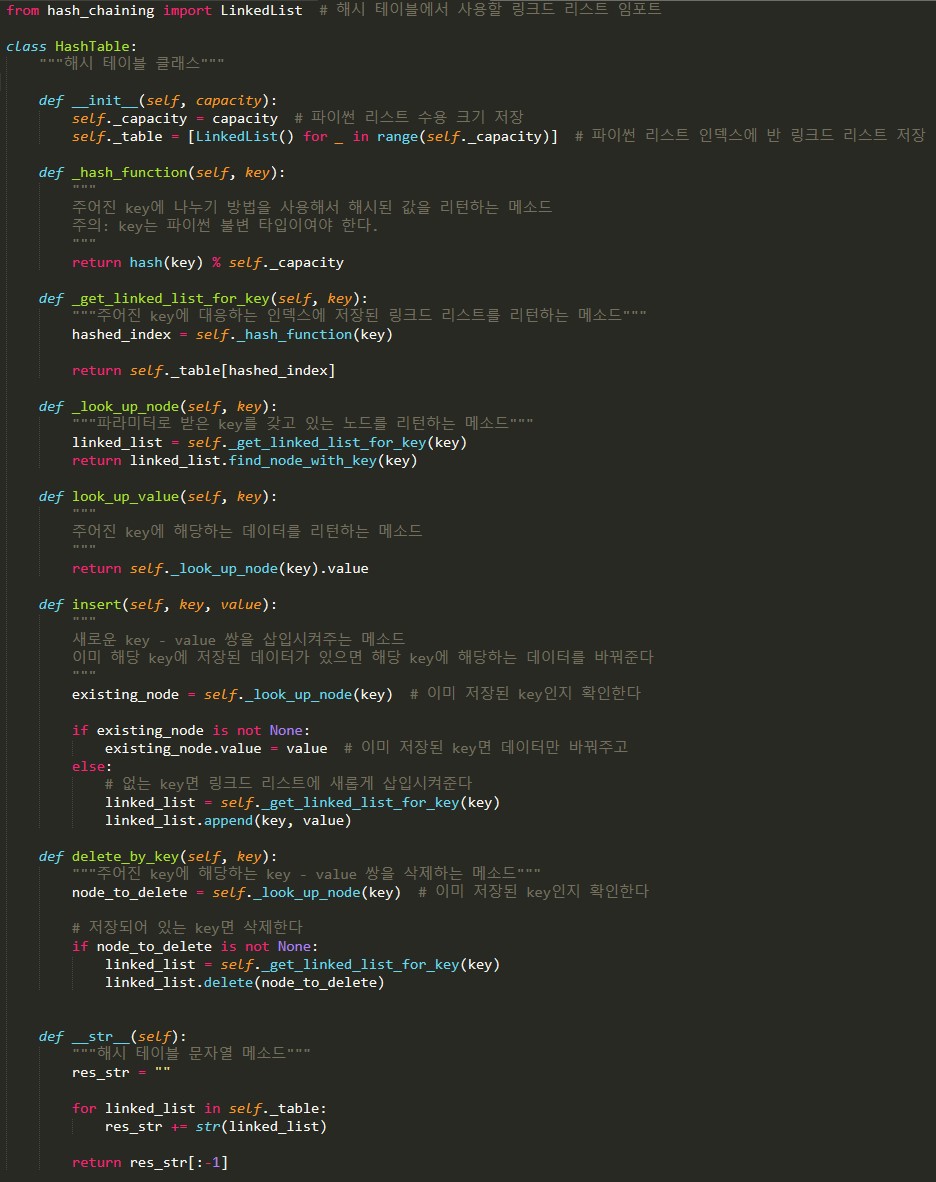
    14. Open Addressing을 이용한 충돌 해결

      • Open Addressing : 충돌이 일어났을 때, 다른 비어 있는 인덱스를 찾아서 데이터를 저장하는 방법

        • 선형 탐사(linear probing)을 통해서 비어있는 인덱스를 찾기

          • 충돌이 일어났을 때, 한 칸씩 다음 인덱스가 비었는지 확인

          • 빈 인덱스를 하나씩 순선대로 선형적으로 찾는 방법

    15. Open Addressing 제곱 탐사

      • 제곱 탐사 (Quadratic Probing)

        • 처음에는 1의 제곱 뒤에 있는 인덱스를 확인하고, 해당 인덱스가 차있는 경우 2의 제곱 뒤에 있는 인덱스를 확인, 또 인덱스가 차있으면 3의 제곱 뒤에 있는 인덱스를 확인...

        • 선형적으로 바로 다음 인덱스들을 확인하지 않고 제곱을 한 값들을 이용하여 인덱스를 찾음

    16. Open Addressing 탐색/삭제 연산

      • 탐색/삭제 : 선형 탐사를 이용하여 데이터를 찾음

        • 해시함수 결과값에서 시작해서 선형 탐사을 하다가 빈 인덱스를 만나면 애초에 저장되지 않았다는 의미가 되므로, 탐색 중단

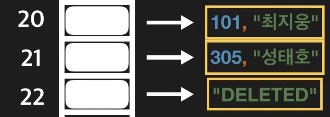
          • 데이터를 찾고 삭제만 하는 경우, 선형 탐사 시 문제가 생길 수 있음 (허리가 끊겨 있어서 탐색하다가 끊긴 곳에서 중단)

          • 삭제의 경우 삭제되었다는 표기를 별도로 해줌 (deleted)

             

             

    17. Open Addressing을 쓰는 해시 테이블 시간 복잡도

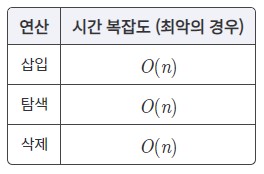
      • 삽입/탐색/삭제 연산 모두 탐사 연산을 포함하고 있음

        • 탐사 염산이 O(n)이므로 모두 O(n)의 시간 복잡도를 가짐

           

           

    18. (중요!) Open Addressing을 쓰는 해시 테이블 평균 시간 복잡도

      • 해시 테이블 연산들을 분석할때는 load factor를 사용

        • load factor (알파) = 해시 테이블 안에 들어있는 데이터 쌍 수 (n)  / 해시 테이블이 사용하는 배열의 크기 (m)

           

          >> 해시 테이블이 얼마나 차있는지를 나타내는 변수

        • 해시 테이블 안에 배열의 크기보다 많은 key-value쌍을 저장할 수 없기 때문에 load factor 알파는 항상 1보다 작다고 가정함

      • Open Addressing을 사용하는 해시 테이블에서 평균적으로 탐사를 해야 되는 횟수(기댓값)은  1/1-알파 보다 작음

        • 모든 알파에 대해서 계산을 하면 성공적으로 인덱스를 찾아봐야하는 인덱스 수는 평균적으로 O(1)

        • 결론적으로, Open Addressing을 사용하든 Chaining을 사용하든 해시 테이블의 모든 연산들을 평균적으로 O(1)로 할 수 있음

    19. 해시 테이블 퀴즈

      • -

  • 추상 자료형

    1. 기능 vs 구현

      • 기능 : 연산이 "무엇"을 하는지에 대한 약속

      • 구현 : 연산의 기능을 "어떻게" 하는지에 대한 구체적 설명

    2. 추상화

      • 추상화는 구현을 몰라도 기능만 알면 프로그래밍을 할 수 있게 해주는 개념

        • 추상화를 하면 이미 쓴 코드를 재활용하고, 개발자들끼리 협력하기 쉬워짐

      • 추상 자료형 (Abstract Data Type)

        • 자료 구조를 추상화 한 것

        • 데이터를 정확히 어떻게 저장하고 어떻게 가져오는지에 대해 신경쓰지 않고, 오직 기능만으로 데이터를 다를 수 있게 해줌

    3. 추상 자료형 vs 자료 구조

      • 추상 자료형

        • 연산의 기능들만 가지고 있음

        • 정확히 어떻게 구현할 것인지에 대한 내용은 포함되어 있지 않음

      • 자료 구조

        • 정확히 데이터를 어떻게 저장할 것인지, 각 연산들을 구체적으로 어떻게 할지 등 모든 것을 묶어 놓은 개념

        • 기능 뿐 아니라 구현에 대한 구체적인 내용도 포함하고 있음

      • 추상 자료형이 필요한 이유?

        • 프로그래밍을 할때 바로 자료구조를 떠올리는 것 보다, 추상 자료형을 떠올리는 것이 더 쉬움

        • 기능을 생각하기는 쉬운데, 매번 구현을 생각하다 보면, 프로그램의 큰 틀을 잡는데 힘들어질 수 있음

        • 추상 자료형을 먼저 생각하면 코드의 흐름에 집중하는 것이 더 쉬워짐

    4. 추상 자료형 vs 자료 구조 현실 비유

      • 기능을 중점적으로 얘기하고 싶을 때, 흐름을 생각할 때 같이 구현에 집중할 필요가 없을땐 추상 자료형을 사용

      • 코드의 성능을 분석하거나 최적화 시켜야 될 때나 성능을 최대로 끓어올리고 싶을 때는 자료 구조를 중심적으로 생각

    5. 리스트 개념

      • 리스트는 데이터간 순서를 유지해주는 대표적인 추상 자료형

        • 접근 연산 : 특정 위치에 있는 데이터를 가지고 오거나 수정한다

        • 탐색 연산 : 특정 조건을 만족하는 데이터를 찾는다

        • 삽입 연산 : 특정 위치에 새로운 데이터를 저장한다

        • 삭제 연산 : 특정 위치에 있는 데이터를 지운다

      • 파이썬은 추상화가 많이 된 고수준 언어로, 많은 자료형 이름이 추상 자료형임 

         

         

        • 개발자들이 리스트를 떠올릴 때 구현을 전혀 몰라도, 기능들만 알아도 사용할 수 있음

           

    6. 리스트 구현

       

      •  

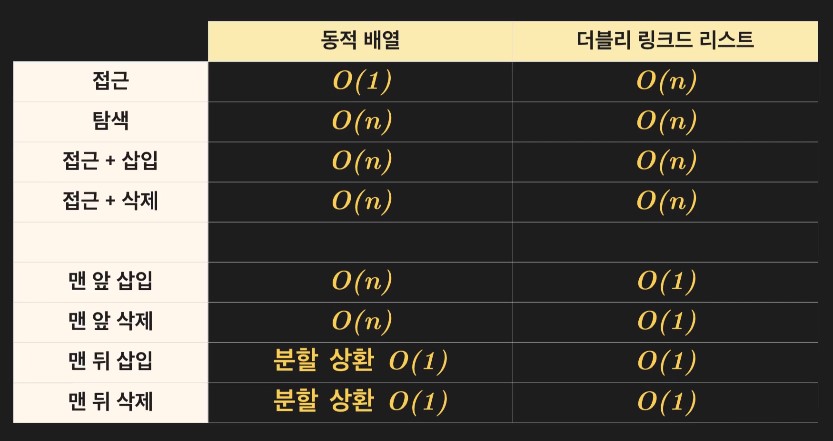
        • 어떤 식의 기능을 원하는가에 따라 자료 구조를 선택하여 설계

        • 파이썬 리스트는 내부적으로 동적 배열로 구현되어 있음

           

    7. 큐 개념

      • 큐( Queue)

        • 데이터 간 순서를 약속하는 자료형

        • 한국어로는 대기열이라고도 함

        • FIFO(First in First out) : 데이터를 삭제할때는 가장 앞에 것만 삭제하고, 데이터를 삽입할때는 가장 뒤에만 삽입 

          • 가장 먼저 들어온 데이터가 가장 먼저 삭제

        • 큐의 연산

          • 맨 뒤 데이터 추가

          • 맨 앞 데이터 삭제

          • 맨 앞 데이터 접근

        • 파이썬에서는 deque라는 자료형을 사용하여 큐를 사용할 수 있음

          • Doubly-ended-queue의 약자

          • 맨 앞과 뒤에 데이터를 삽입하고 삭제할 수 있게 해주는 자료형

             

             

    8. 큐 구현

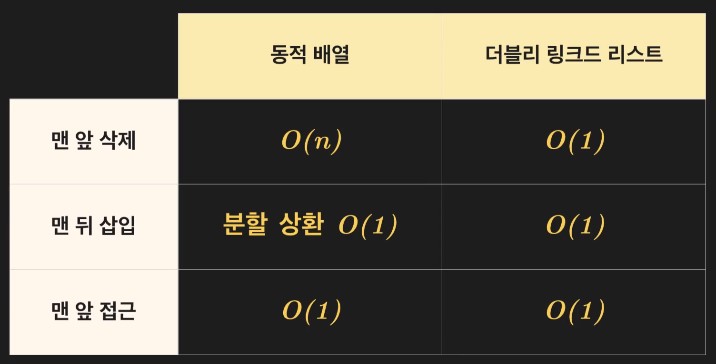
      • 리스트와 마찬가지로, 동적 배열이나 링크드 리스트로 구현할 수 있음

         

         

      • 파이썬 deque는 내부적으로 더블리 링크드 리스트로 구현되어 있음

    9. 서비스 센터 문의 처리

      • -

    10. 스택 개념

      • 스택 (stack)

        • 데이터 간 순서를 약속하는 추상 자료형

        • LIFO (Last-in-first-out) : 가장 마지막에 들어온 데이터가 가장 먼저 삭제됨

        • 스택의 연산

          • 맨 뒤 데이터 추가

          • 맨 뒤 데이터 삭제

          • 맨 뒤 데이터 접근

        • 파이썬 자료형 가운데 스택의 이름을 갖는 자료형은 없음

          • 큐와 마찬가지로 deque를 사용

             

             

    11. 스택 구현

       

        • 리스트를 사용하면 동적 배열,  deque를 사용하면 더블리 링크드 리스트를 사용할 수 있음

           

    12. 괄호 짝 확인하기

      • -

    13. 딕셔너리

      • 딕셔너리 (= "맵"이라고도 부름)

        • 앞선 추상 자료형들과 달리 저장하는 데이터 간의 순서 관계를 약속하지 않음

        • 딕셔너리의 연산

          • key-value 데이터 쌍 삽입

          • key를 이용한 데이터 탐색

          • key를 이용한 데이터 삭제

             

             

        • 딕셔너리의 구현

           

           

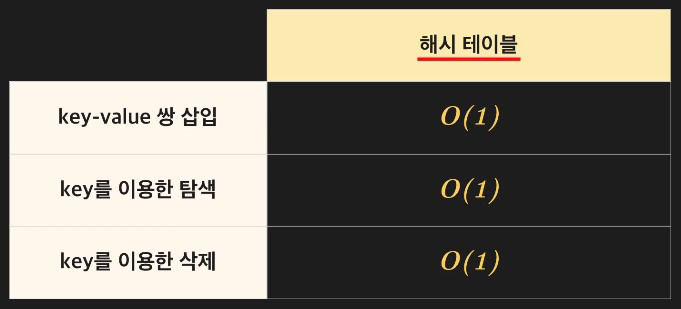
    14. 세트 개념

      • 세트 (집합)

        • 순서에 상관없이 그냥 데이터를 저장할 수 있는 추상 자료형

        • 세트의 연산

          • 삽입 : 데이터를 저장할 수 있음 (중복 데이터 x)

          • 탐색 : 데이터가 저장됐는지 확인할 수 있음

          • 삭제 : 저장한 데이터를 지울 수 있음

             

             

          • 단순히 데이터를 저장하고 저장한 데이터를 탐색하고 원하는 데이터를 삭제하고 싶을 때 사용하면 좋음

             

    15. 세트 구현

      • 세트는 주로 해시테이블을 통해 구현

        • 처음에 저장할 때부터 인덱스에 key만 저장

           

           

    16. 파이썬 자료형 주요 시간 복잡도 정리

      •  

         

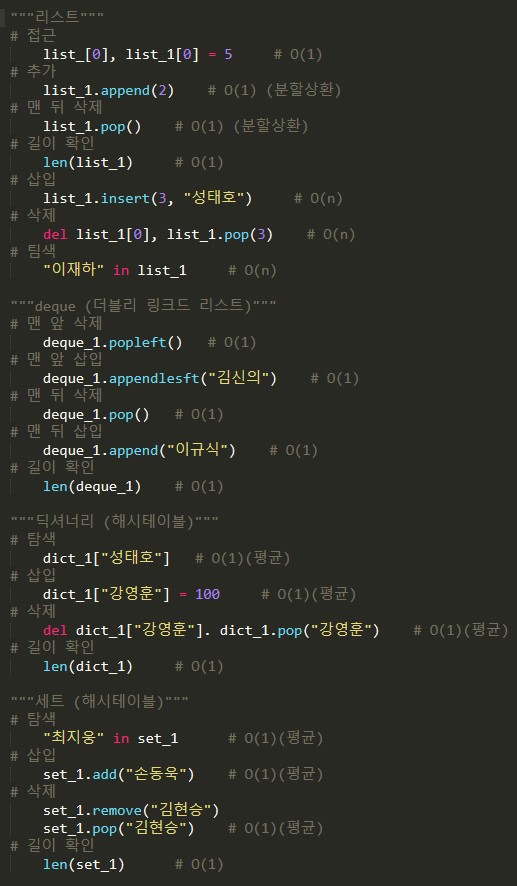
    17. 파이썬 자료형 잘 고르기

      • 자료형을 잘 고른다는 것은 현재 자신이 데이터에 하고 싶은 연산들이 뭐가 있고 얼마나 걸릴지에 대해서 잘 생각하는 것

        • 초급자의 수준을 넘어서기 위해서는 파이썬 자료형 뒤에 가려진 자료 구조를 떠올릴 수 있어야 됨 (각 연산의 시간복잡도)

      • 어떤 자료형을 사용할 건지 잘 고르는 건 결국 어떤 자료 구조를 쓸 건지 고르는 것과 비슷

        • 데이터에 어떤 관계가 필요하고 어떤 기능들을 사용할 건지 잘 생각하면 더 효율적인 프로그램을 쓸 수 있음

    18. 추상 자료형 퀴즈

      • -

 

저작자표시 (새창열림)